如图所示是甲乙两个工程队完成某项工程的进度图,首先是甲独做了10天,然后两队合做,完成剩下的工程.
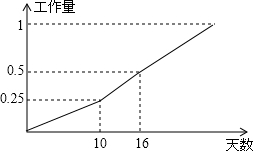
(1)甲队单独完成这项工程,需要多少天?
(2)求乙队单独完成这项工程需要的天数;
(3)实际完成的时间比甲独做所需的时间提前多少天?
相关知识点
推荐套卷
如图所示是甲乙两个工程队完成某项工程的进度图,首先是甲独做了10天,然后两队合做,完成剩下的工程.

(1)甲队单独完成这项工程,需要多少天?
(2)求乙队单独完成这项工程需要的天数;
(3)实际完成的时间比甲独做所需的时间提前多少天?