如图，已知四棱锥P-ABCD，底面ABCD为边长为2的菱形，PA⊥平面ABCD，∠ABC=60°，E，F分别是BC，PC的中点．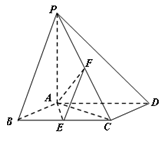
（Ⅰ）判定 AE与PD是否垂直，并说明理由；
（Ⅱ）若PA=2，求二面角E-AF-C的余弦值．
，且
，求
的值。
,求cosθ的值.
的对称轴方程为：
，设向量
，
.
和
的取值范围；
时，求不等式
的解集.
的最大值为3，最小值为
.
的值；
时，函数
的值域.相关知识点
推荐套卷
如图，已知四棱锥P-ABCD，底面ABCD为边长为2的菱形，PA⊥平面ABCD，∠ABC=60°，E，F分别是BC，PC的中点．
（Ⅰ）判定 AE与PD是否垂直，并说明理由；
（Ⅱ）若PA=2，求二面角E-AF-C的余弦值．
粤公网安备 44130202000953号