一辆快车从甲地开往乙地，一辆慢车从乙地开往甲地，两车同时出发，设慢车离乙地的距离为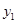
（km），快车离乙地的距离为
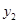（km），慢车行驶时间为x（h），两车之间的距离为S（km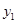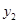），，与x的函数关系图象如图（1）所示，S与x的函数关系图象如图（2）所示：
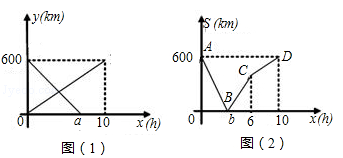
（1）图中的a= ，b= ；
（2）求S关于x的函数关系式；
（3）甲、乙两地间依次有E、F两个加油站，相距200km，若慢车进入E站加油时，快车恰好进入F站加油．求E加油站到甲地的距离．
相关试题
如图，在正方形网格中，△ABC各顶点都在格点上，点A，C的坐标分别为（﹣5，1）、（﹣1，4），结合所给的平面直角坐标系解答下列问题：
（1）画出△ABC关于y轴对称的△A1B1C1；
（2）画出△ABC关于原点O对称的△A2B2C2；
（3）点C1的坐标是；点C2的坐标是；过C、C1、C2三点的圆的圆弧
的长是（保留π）．
，0），直线
与x轴交于点F，与y轴交于点B，直线l∥AB且交y轴于点C，交x轴于点D，点A关于直线l的对称点为A′，连接AA′、A′D．直线l从AB出发，以每秒1个单位的速度沿y轴正方向向上平移，设移动时间为t．
相关知识点
推荐套卷
粤公网安备 44130202000953号