如图，用三个正方形①、2个正方形②、1个正方形③和缺了一个角的长方形④，恰好拼成一个大长方形．根据图示数据，解答下列问题：
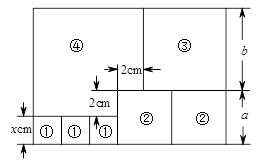
（1）用含x的代数式表示：a= cm，b= cm；
（2）用含x的代数式表示大长方形的周长，并求x=3时大长方形的周长．
相关试题
小明和小刚用如图的两个转盘做配紫色的游戏，游戏规则是：分别旋转两个转盘，若其中的一个转盘转出了红色，另一个转出了蓝色，则可以配成紫色。此时小刚得1分，否则小明得1分。此游戏规则公平吗？请说明理由。
如图是椒江某公园一圆形喷水池，水流在各方向沿形状相同的抛物线落下。建立如图所示的坐标系，如果喷头所在处A（0，1.25），水流路线最高处B（1，2.25），求该抛物线的解析式.
粤公网安备 44130202000953号