有三张卡片(背面完全相同)分别写有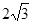 、
、 、
、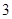 ,把它们背面朝上洗匀后,小明从中抽取一张,记下这个数后放回洗匀,小白又从中抽出一张.
,把它们背面朝上洗匀后,小明从中抽取一张,记下这个数后放回洗匀,小白又从中抽出一张.
(1)小明抽取的卡片为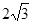 的概率是 ;两人抽取的卡片都为
的概率是 ;两人抽取的卡片都为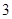 的概率是 .
的概率是 .
(2)小刚为他们俩设计了一个游戏规则:若两人抽取的卡片上两数之积是有理数,则小明获胜,否则小白获胜.你认为这个游戏规则对谁有利?请说明理由.
相关知识点
推荐套卷
有三张卡片(背面完全相同)分别写有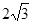 、
、 、
、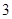 ,把它们背面朝上洗匀后,小明从中抽取一张,记下这个数后放回洗匀,小白又从中抽出一张.
,把它们背面朝上洗匀后,小明从中抽取一张,记下这个数后放回洗匀,小白又从中抽出一张.
(1)小明抽取的卡片为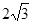 的概率是 ;两人抽取的卡片都为
的概率是 ;两人抽取的卡片都为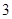 的概率是 .
的概率是 .
(2)小刚为他们俩设计了一个游戏规则:若两人抽取的卡片上两数之积是有理数,则小明获胜,否则小白获胜.你认为这个游戏规则对谁有利?请说明理由.