作图题:
(1)如图,在图1所给方格纸中,每个小正方形边长都是1,标号为①②③的三个三角形均为格点三角形(顶点在方格顶点处),请按要求将图2中的指定图形分割成三个三角形,使它们与标号为①②③的三个三角形分别对应全等.(分割线画成实线.)
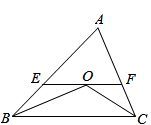
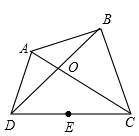
(2)如图3,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
①在图中画出与△ABC关于直线L成轴对称的△A′B′C′;
②请直线L上找到一点P,使得PC + PB的距离之和最小..
相关知识点
推荐套卷

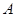 种果汁原料和
种果汁原料和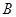 种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制
种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制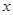 千克,两种饮料的成本总额为
千克,两种饮料的成本总额为 元.
元.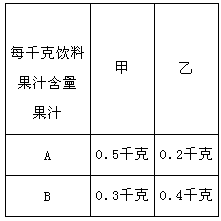

 粤公网安备 44130202000953号
粤公网安备 44130202000953号