如图，在平面直角坐标系中，⊙A与x轴相交于C（﹣2，0），D（﹣8，0）两点，与y轴相切于点B（0，4）．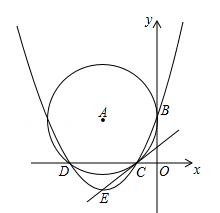
（1）求经过B，C，D三点的抛物线的函数表达式；
（2）设抛物线的顶点为E，求证：直线CE与⊙A相切；
（3）在x轴下方的抛物线上，是否存在一点F，使△BDF面积最大，最大值是多少？并求出点F的坐标．
相关试题
如图，O是直线AB上一点，OC为任一条射线，OD平分∠BOC，OE平分∠AOC。
（1）写出图中∠AOD与∠BOE的补角；
（2）试说明∠COD与∠COE具有怎样的数量关系。
。
、3、-2.5 、
粤公网安备 44130202000953号