我们学习过:在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动叫做旋转,这个定点称为旋转中心,旋转的角度称为旋转角.
(1)如图(1),△ABC经过旋转得到△DEF.试用直尺和圆规作出旋转中心 (保留作图痕迹,不写作法) ;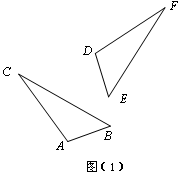
(2)如图(2),正方形ABCD中,E、F分别为CD、AD的中点,连接BE、CF,△BCE按逆时针方向旋转后得到△CDF,则旋转中心为 (请在图中画出该点,标上字母,并回答),旋转的最小角度为 .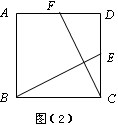
相关知识点
推荐套卷
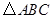 的
的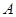 点平移到
点平移到 ,
,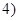
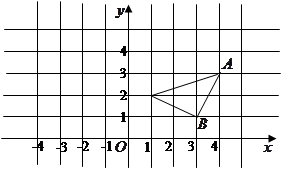
 ,
,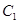 的坐标
的坐标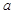 ∥
∥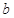 .直线
.直线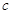 与直线
与直线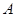 、点
、点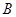 ,
,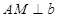 ,垂足为点
,垂足为点 ,若
,若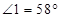 ,求
,求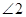 的度数.
的度数.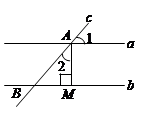
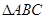 中,
中,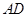 是
是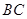 边上的高,
边上的高,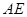 是
是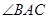 平分线.
平分线.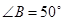 ,
,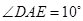 。
。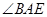 的度数;
的度数;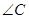 的度数.
的度数.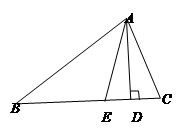
 粤公网安备 44130202000953号
粤公网安备 44130202000953号