(资阳)已知直线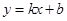 (
(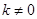 )过点F(0,1),与抛物线
)过点F(0,1),与抛物线 相交于B、C两点.
相交于B、C两点.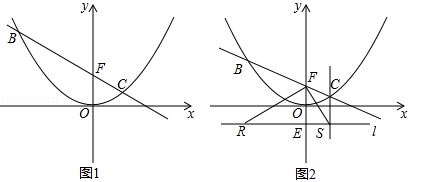
(1)如图1,当点C的横坐标为1时,求直线BC的解析式;
(2)在(1)的条件下,点M是直线BC上一动点,过点M作y轴的平行线,与抛物线交于点D,是否存在这样的点M,使得以M、D、O、F为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由;
(3)如图2,设B(m,n)(m<0),过点E(0,﹣1)的直线l∥x轴,BR⊥l于R,CS⊥l于S,连接FR、FS.试判断△RFS的形状,并说明理由.
(资阳)已知直线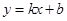 (
(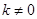 )过点F(0,1),与抛物线
)过点F(0,1),与抛物线 相交于B、C两点.
相交于B、C两点.
(1)如图1,当点C的横坐标为1时,求直线BC的解析式;
(2)在(1)的条件下,点M是直线BC上一动点,过点M作y轴的平行线,与抛物线交于点D,是否存在这样的点M,使得以M、D、O、F为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由;
(3)如图2,设B(m,n)(m<0),过点E(0,﹣1)的直线l∥x轴,BR⊥l于R,CS⊥l于S,连接FR、FS.试判断△RFS的形状,并说明理由.