甲、乙两车从A地出发沿同一路线驶向B地，甲车先出发匀速驶向B地．40分钟后，乙车出发，匀速行驶一段时间后，在途中的货站装货耗时半小时，由于满载货物，为了行驶安全，速度减少了50千米/时，结果与甲车同时到达B地．甲乙两车距A地的路程y（千米）与乙车行驶时间x（小时）之间的函数图象如图所示．
请结合图象信息解答下列问题：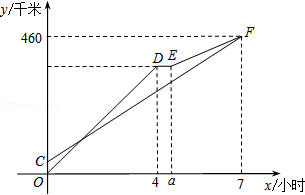
（1）直接写出a的值，并求甲车的速度；
（2）求图中线段EF所表示的y与x的函数关系式，并直接写出自变量x的取值范围；
（3）乙车出发多少小时与甲车相距15千米？直接写出答案．
如图：已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E、F．
（1）求证：DE=DF；
（2）若
，BE=1，求△ABC的周长．
已知，在平面直角坐标系中，直线y=2x+3与直线y=﹣2x﹣1交于点C．
（1）求两直线与y轴交点A，B的坐标；
（2）求点C的坐标；
（3）求△ABC的面积．
如图，在平面直角坐标系
中，A(1,2)，B(3,1)，C(-2，-1)．
（1）在图中作出
关于
轴的对称图形
．
（2）写出点
的坐标（直接写答案）．
A 1 ______________
B 1 ______________
C 1 ______________
使得函数值为零的自变量的值称为函数的零点。例如，对于函数
，令y=0，可得x=1，我们就说1是函数的零点。
己知函数
(
m为常数)。
（1）当=0时，求该函数的零点；
（2）证明：无论取何值，该函数总有两个零点；
（3）设函数的两个零点分别为
和
，且
，此时函数图象与x轴的交点分别为A、B(点A在点B左侧)，点M在直线
上，当MA+MB最小时，求直线AM的函数解析式。
如图1至图4中，两平行线AB、CD间的距离均为6，点M为AB上一定点．
思考：
如图1，圆心为0的半圆形纸片在AB，CD之间（包括AB，CD），其直径MN在AB上，MN=8，点P为半圆上一点，设∠MOP=α。
当α= 度时，点P到CD的距离最小，最小值为 。
探究一：
在图1的基础上，以点M为旋转中心，在AB，CD 之间顺时针旋转该半圆形纸片，直到不能再转动为止，如图2，得到最大旋转角∠BMO= 度，此时点N到CD的距离是 。
探究二：
将如图1中的扇形纸片NOP按下面对α的要求剪掉，使扇形纸片MOP绕点M在AB，CD之间顺时针旋转。
（1）如图3，当α=60°时，求在旋转过程中，点P到CD的最小距离，并请指出旋转角∠BMO的最大值；
（2）如图4，在扇形纸片MOP旋转过程中，要保证点P能落在直线CD上，请确定α的最大值。
粤公网安备 44130202000953号