某校为了丰富学生的第二课堂,对学生参与演讲、舞蹈、书法和摄影活动的兴趣情况进行调查,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中最感兴趣的一项),对调查结果进行统计后,绘制了如下两个统计图:
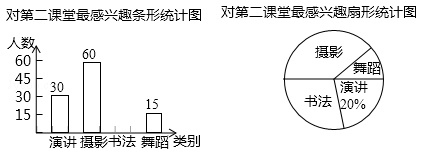
(1)此次调查抽取的学生人数m=
(2)若该校有3000名学生,请根据以上数据估计该校对"书法"最感兴趣的学生人数.
相关知识点
推荐套卷
某校为了丰富学生的第二课堂,对学生参与演讲、舞蹈、书法和摄影活动的兴趣情况进行调查,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中最感兴趣的一项),对调查结果进行统计后,绘制了如下两个统计图:

(1)此次调查抽取的学生人数m=
(2)若该校有3000名学生,请根据以上数据估计该校对"书法"最感兴趣的学生人数.