已知，在平面直角坐标系中，点P（0，2），以P为圆心，OP为半径的半圆与y轴的另一个交点是C，一次函数
（m为实数）的图象为直线l，l分别交x轴，y轴于A，B两点，如图1．
B点坐标是 （用含m的代数式表示），∠ABO= °
若点N是直线AB与半圆CO的一个公共点（两个公共点时，N为右侧一点），过点N作⊙P的切线交x轴于点E，如图2．
①是否存在这样的m的值，使得△EBN是直角三角形。若存在，求出m的值；若不存在，请说明理由．
②当
=
时，求m的值
相关试题
．
，其中
．
（结果保留π）如图，一次函数y=x﹣5分别交x轴、y轴于A、B两点，二次函数y=﹣x2+bx+c的图象经过A、B两点．
（1）求二次函数的解析式；
（2）设D、E是线段AB上异于A、B的两个动点（E点位于D点上方），DE=
．
①若点D的横坐标为t，用含t的代数式表示D、E的坐标；
②抛物线上是否存在点F，使点F与点D关于x轴对称，如果存在，请求出△AEF的面积；如果不存在，请说明理由．
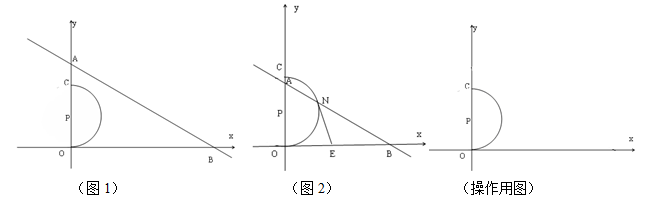
相关知识点
推荐套卷
粤公网安备 44130202000953号