有这样一个问题:探究函数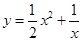 的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数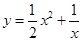 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数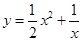 的自变量x的取值范围是____;
的自变量x的取值范围是____;
(2)下表是y与x的几组对应值.
求m的值:
(3)如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象:
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是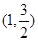 ,结合函数的图象,写出该函数的其它性质(一条即可):_________.
,结合函数的图象,写出该函数的其它性质(一条即可):_________.
相关知识点
推荐套卷
 (
( 为常数,且
为常数,且 )的图像与反比例函数
)的图像与反比例函数 的图像交于
的图像交于 ,
, 两点.
两点. 向下平移
向下平移 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求 的值.
的值.
 ,其中
,其中 ,
, .
. .
.

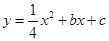 与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线
与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线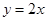 于点C;
于点C;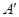 的坐标,判定点
的坐标,判定点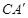 于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.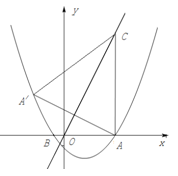
 粤公网安备 44130202000953号
粤公网安备 44130202000953号