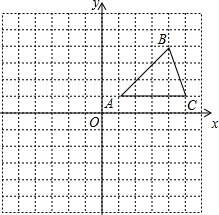
在平面直角坐标系中， 的位置如图所示（每个小方格都是边长为1个单位长度的正方形）．
（1）将 沿 轴方向向左平移6个单位，画出平移后得到的△ ；
（2）将 绕着点 顺时针旋转 ，画出旋转后得到的△ ，并直接写出点 、 的坐标．
相关试题
如图，在△ABC中，AB=AC，点D是BC的中点，DE⊥AC于点E，DG⊥AB于点G，EK⊥AB于点K，GH⊥AC于点H、EK和GH相交于点F．
求证：GE与FD互相垂直平分．
推荐套卷
在平面直角坐标系中， 的位置如图所示（每个小方格都是边长为1个单位长度的正方形）．
（1）将 沿 轴方向向左平移6个单位，画出平移后得到的△ ；
（2）将 绕着点 顺时针旋转 ，画出旋转后得到的△ ，并直接写出点 、 的坐标．
如图，在△ABC中，AB=AC，点D是BC的中点，DE⊥AC于点E，DG⊥AB于点G，EK⊥AB于点K，GH⊥AC于点H、EK和GH相交于点F．
求证：GE与FD互相垂直平分．
粤公网安备 44130202000953号