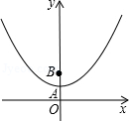
如图,在平面直角坐标系 中,抛物线 与 轴相交于点 ,点 与点 关于点 对称
(1)填空:点 的坐标是 ;
(2)过点 的直线 (其中 与 轴相交于点 ,过点 作直线 平行于 轴, 是直线 上一点,且 ,求线段 的长(用含 的式子表示),并判断点 是否在抛物线上,说明理由;
(3)在(2)的条件下,若点 关于直线 的对称点 恰好落在该抛物线的对称轴上,求此时点 的坐标.
推荐套卷
如图,在平面直角坐标系 中,抛物线 与 轴相交于点 ,点 与点 关于点 对称
(1)填空:点 的坐标是 ;
(2)过点 的直线 (其中 与 轴相交于点 ,过点 作直线 平行于 轴, 是直线 上一点,且 ,求线段 的长(用含 的式子表示),并判断点 是否在抛物线上,说明理由;
(3)在(2)的条件下,若点 关于直线 的对称点 恰好落在该抛物线的对称轴上,求此时点 的坐标.
