抛物线y=ax2+3交x轴于A(-4,0)、B两点,交y轴于C.将一把宽度为1.2的直尺如图放置在直角坐标系中,使直尺边A′D′∥BC,直尺边A′D′交x轴于E,交AC于F,交抛物线于G,直尺另一边B′C′交x轴于D.当点D与点A重合时,把直尺沿x轴向右平移,当点E与点B重合时,停止平移,在平移过程中,△FDE的面积为S.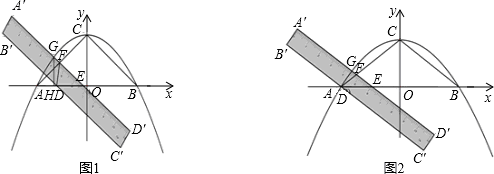
(1)请你求出S的最大值及抛物线解析式;
(2)在直尺平移过程中,直尺边B′C′上是否存在一点P,使点P、D、E、F构成的四边形这菱形,若存在,请你求出点P坐标;若不存在,请说明理由;
(3)过G作GH⊥x轴于H
①在直尺平移过程中,请你求出GH+HO的最大值;
②点Q、R分别是HC、HB的中点,请你直接写出在直尺平移过程中,线段QR扫过的图形的面积和周长.
相关知识点
推荐套卷



 粤公网安备 44130202000953号
粤公网安备 44130202000953号