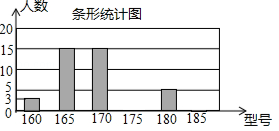
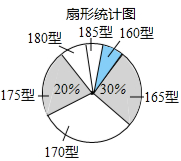
我市某中学艺术节期间,向全校学生征集书画作品.九年级美术王老师从全年级14个班中随机抽取了A、B、C、D共4个班,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.
(1)王老师采取的调查方式是 (填“普查”或“抽样调查”).
(2)王老师所调查的4个班征集到作品共 件,其中B班征集到作品 件.
(3)请把图2补充完整;
(4)王老师所调查的四个班平均每个班征集作品多少件?请估计全年级共征集到作品多少件?
相关知识点
推荐套卷
 .
.
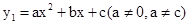 过点A(1,0),顶点为B,且抛物线不经过第三象限。
过点A(1,0),顶点为B,且抛物线不经过第三象限。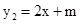 经过点B,且于该抛物线交于另一点C(
经过点B,且于该抛物线交于另一点C(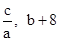 ),求当x≥1时y1的取值范围。
),求当x≥1时y1的取值范围。
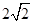 时(如图),求证:CD是⊙O的切线;
时(如图),求证:CD是⊙O的切线; 粤公网安备 44130202000953号
粤公网安备 44130202000953号