阅读下面的材料:
如果函数
满足:对于自变量
的取值范围内的任意
,
,
(1)若
,都有
,则称
是增函数;
(2)若
,都有
,则称
是减函数.
例题:证明函数
是减函数.
证明:设
,
.
,
,
.
.即
.
.
函数
是减函数.
根据以上材料,解答下面的问题:
已知函数
,
,
(1)计算:
,
;
(2)猜想:函数
是 函数(填“增”或“减”
;
(3)请仿照例题证明你的猜想.
 中,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接BE,∠F=45°.
中,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接BE,∠F=45°.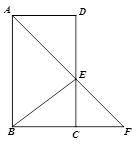
 中,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接BE,∠F=45°.
中,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接BE,∠F=45°.