(本小题满分12分)某学校举行联欢会,所有参演的节目都由甲、乙、丙三名专业老师投票决定是否获奖.甲、乙、丙三名老师都有“获奖”、“待定”、“淘汰”三类票各一张.每个节目投票时,甲、乙、丙三名老师必须且只能投一张票,每人投三类票中的任何一类票的概率都为 ,且三人投票相互没有影响.若投票结果中至少有两张“获奖”票,则决定该节目最终获一等奖;否则,该节目不能获一等奖.
,且三人投票相互没有影响.若投票结果中至少有两张“获奖”票,则决定该节目最终获一等奖;否则,该节目不能获一等奖.
(1)求某节目的投票结果是最终获一等奖的概率;
(2)求该节目投票结果中所含“获奖”和“待定”票票数之和 的分布列及数学期望.
的分布列及数学期望.
相关知识点
推荐套卷
 (千米/小时)与所用时间
(千米/小时)与所用时间 (小时)的函数关系如图所示,其中
(小时)的函数关系如图所示,其中 .
.
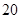 千米,
千米,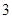 小时后两车相遇.
小时后两车相遇. 、
、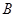 ,它们相距
,它们相距 千米,当客车进入
千米,当客车进入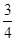 .求线段CF的长.
.求线段CF的长.
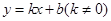 的图象与反比例函数
的图象与反比例函数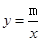 的图象交于一、三象限内的A、B两点,直线AB与x轴交于点C,点B的坐标为(-6,n),线段OA=5,E为x轴正半轴上一点,且tan∠AOE=
的图象交于一、三象限内的A、B两点,直线AB与x轴交于点C,点B的坐标为(-6,n),线段OA=5,E为x轴正半轴上一点,且tan∠AOE=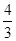 ,求△AOB的面积.
,求△AOB的面积.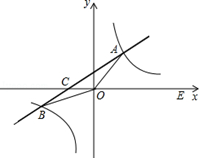
 ,其中
,其中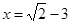 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号