设各项均为正数的等比数列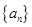 的公比为
的公比为 ,
,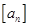 表示不超过实数
表示不超过实数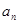 的
的
最大整数(如 ),设
),设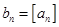 ,数列
,数列 的前
的前 项和为
项和为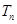 ,
,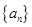 的前
的前 项和为
项和为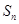 .
.
(Ⅰ)若 ,求
,求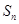 及
及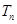 ;
;
(Ⅱ)若对于任意不超过2015的正整数 ,都有
,都有 ,证明:
,证明: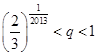 .
.
相关知识点
推荐套卷
设各项均为正数的等比数列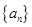 的公比为
的公比为 ,
,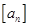 表示不超过实数
表示不超过实数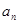 的
的
最大整数(如 ),设
),设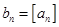 ,数列
,数列 的前
的前 项和为
项和为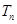 ,
,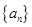 的前
的前 项和为
项和为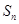 .
.
(Ⅰ)若 ,求
,求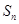 及
及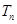 ;
;
(Ⅱ)若对于任意不超过2015的正整数 ,都有
,都有 ,证明:
,证明: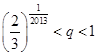 .
.