(本小题10分)已知抛物线 .
.
(1)求它的对称轴与 轴交点
轴交点 的坐标;
的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与 轴的交点为
轴的交点为 ,
, ,与
,与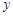 轴的交点为
轴的交点为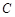 ,若
,若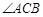 =90°,求此时抛物线的解析式;
=90°,求此时抛物线的解析式;
(3)若点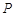 (
(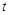 ,
,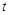 )在抛物线上,则称点
)在抛物线上,则称点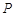 为抛物线的不动点.将抛物线
为抛物线的不动点.将抛物线 进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线
进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线 上,请说明理由.
上,请说明理由.
相关知识点
推荐套卷
(本小题10分)已知抛物线 .
.
(1)求它的对称轴与 轴交点
轴交点 的坐标;
的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与 轴的交点为
轴的交点为 ,
, ,与
,与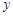 轴的交点为
轴的交点为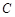 ,若
,若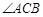 =90°,求此时抛物线的解析式;
=90°,求此时抛物线的解析式;
(3)若点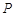 (
(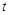 ,
,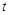 )在抛物线上,则称点
)在抛物线上,则称点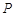 为抛物线的不动点.将抛物线
为抛物线的不动点.将抛物线 进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线
进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线 上,请说明理由.
上,请说明理由.