如图，在平面直角坐标中，点A的坐标为（1，1），OA=AC，∠OAC=90°，点D为x轴上一动点．以AD为边在AD的右侧作正方形ADEF．
（1）当点D在线段OC上时（不与点O、C重合），则线段CF与OD之间的数量关系为 ；位置关系为 ，
（2）当点D在线段OC的延长线上时，（1）中的结论是否成立？若成立，请说明理由；若不成立，请举一反例；
（3）设D点坐标为（t，0），当D点从O点运动到C点时，用含t的代数式表示E点坐标，并直接写出E点所经过的路径长．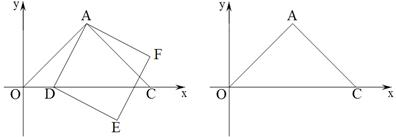
相关试题
如图，已知AB⊥AC，AB=AC，DE过点A，且CD⊥DE，BE⊥DE，垂足分别为点D，E．
（1）∠DCA与∠EAB相等吗？说明理由；
（2）△ADC与△BEA全等吗？说明理由．
如图，在△ABC中，∠ACB＝90°，AC＝BC＝AD
（1）作∠A的角平分线交CD于E;
（2）过B作CD的垂线，垂足为F;
（3）请写出图中一对全等三角形（不添加任何字母）并证明．
推荐套卷
粤公网安备 44130202000953号