（本小题满分12分）已知数列{an}，{bn}满足：a1b1＋a2b2＋a3b3＋…＋anbn＝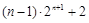
（
）.
（Ⅰ）若{bn }是首项为1，公比为2的等比数列，求数列{an}的前n项和Sn；
（Ⅱ）若{an}是等差数列，且an≠0，问：{bn}是否是等比数列？若是，求{an}和{bn}的通项公式；若不是，请说明理由．
相关试题
;
.
,b=9.求：
.
≤a≤
R,f(x)=f(x+1)+f(x-1)恒成立.推荐套卷
（本小题满分12分）已知数列{an}，{bn}满足：a1b1＋a2b2＋a3b3＋…＋anbn＝（）.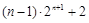
（Ⅰ）若{bn }是首项为1，公比为2的等比数列，求数列{an}的前n项和Sn；
（Ⅱ）若{an}是等差数列，且an≠0，问：{bn}是否是等比数列？若是，求{an}和{bn}的通项公式；若不是，请说明理由．
粤公网安备 44130202000953号