某市城调队就本地居民的月收入调查了10000人, 并根据所得数据画出了样本的频率分布直方图(每个分组包括左端点, 不包括右端点, 如第一组表示收入在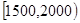 , 单位: 元).
, 单位: 元).
(Ⅰ)求随机抽取一位居民,估计该居民月收入在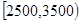 的概率,并估计这10000人的人均月收入;
的概率,并估计这10000人的人均月收入;
(Ⅱ)若将频率视为概率,从本地随机抽取3位居民(看作有放回的抽样),求月收入在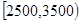 上居民人数
上居民人数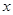 的数学期望.
的数学期望.
推荐套卷
某市城调队就本地居民的月收入调查了10000人, 并根据所得数据画出了样本的频率分布直方图(每个分组包括左端点, 不包括右端点, 如第一组表示收入在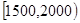 , 单位: 元).
, 单位: 元).
(Ⅰ)求随机抽取一位居民,估计该居民月收入在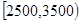 的概率,并估计这10000人的人均月收入;
的概率,并估计这10000人的人均月收入;
(Ⅱ)若将频率视为概率,从本地随机抽取3位居民(看作有放回的抽样),求月收入在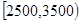 上居民人数
上居民人数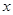 的数学期望.
的数学期望.