如图，在Rt△ABC中，∠C=90°，点P为AC边上的一点，将线段AP绕点A顺时针方向旋转（点P对应点P′），当AP旋转至AP′⊥AB时，点B、P、P′恰好在同一直线上，此时作P′E⊥AC于点E．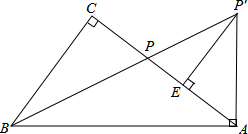
（1）求证：∠CBP=∠ABP；
（2）求证：AE=CP；
（3）当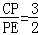
，BP′=5
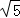时，求线段AB的长．
如图，在Rt△ABC中，∠C=90°，点P为AC边上的一点，将线段AP绕点A顺时针方向旋转（点P对应点P′），当AP旋转至AP′⊥AB时，点B、P、P′恰好在同一直线上，此时作P′E⊥AC于点E．
（1）求证：∠CBP=∠ABP；
（2）求证：AE=CP；
（3）当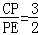，BP′=5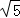时，求线段AB的长．
﹣1＞
，并在数轴上把解集表示出来．
，并把它的解集在数轴上表示出来，再写出这个不等式的最小整数解．
．
．
，并把它的解集在数轴上表示出来．
粤公网安备 44130202000953号