（满分12分）
（1）已知△ABC三个顶点的坐标分别为A（4，1），B（0，3），C（2，4），边AC的中点为D，求AC边上中线BD所在的直线方程并化为一般式；
（2）已知圆C的圆心是直线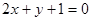
和
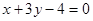的交点上且与直线
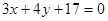相切,求圆C的方程．
，
，
，其中
，
，
与
的夹角
，
与
，且
，求
的值。
，
，
，
。
是否共线？请说
明理由。
的最大值。
中，已知
，
中，
、
、
所对的边分别为
、
、
，
，
，
，求
的值。相关知识点
推荐套卷
（满分12分）
（1）已知△ABC三个顶点的坐标分别为A（4，1），B（0，3），C（2，4），边AC的中点为D，求AC边上中线BD所在的直线方程并化为一般式；
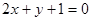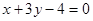（2）已知圆C的圆心是直线和的交点上且与直线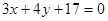相切,求圆C的方程．
粤公网安备 44130202000953号