已知数列{an}满足a1=1,a2=3,且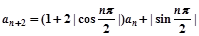 ,
, .
.
(1)证明:数列{a2k}(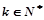 )为等比数列;
)为等比数列;
(2)求数列{an}的通项公式;
(3)设 (λ为非零整数).试确定λ的值,使得对任意
(λ为非零整数).试确定λ的值,使得对任意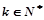 都有
都有 成立.
成立.
相关知识点
推荐套卷
已知数列{an}满足a1=1,a2=3,且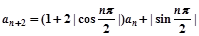 ,
, .
.
(1)证明:数列{a2k}(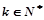 )为等比数列;
)为等比数列;
(2)求数列{an}的通项公式;
(3)设 (λ为非零整数).试确定λ的值,使得对任意
(λ为非零整数).试确定λ的值,使得对任意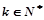 都有
都有 成立.
成立.