如图1,在平面直角坐标系中,抛物线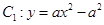 (
(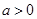 )经过点
)经过点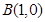 ,顶点为
,顶点为 .
.
(1)求抛物线 的解析式;
的解析式;
(2)如图2,先将抛物线 向上平移使其顶点在原点
向上平移使其顶点在原点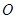 ,再将其顶点沿直线
,再将其顶点沿直线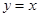 平移得到抛物线
平移得到抛物线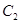 ,设抛物线
,设抛物线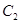 与直线
与直线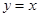 交于
交于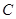 、
、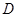 两点,求线段
两点,求线段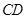 的长.
的长.
(3)在图1中将抛物线 绕点
绕点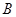 旋转
旋转 后得到抛物线
后得到抛物线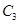 ,直线
,直线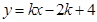 总经过一个定点
总经过一个定点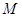 ,若过定点
,若过定点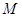 的直线
的直线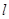 与抛物线
与抛物线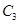 只有一个公共点,求直线
只有一个公共点,求直线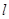 的解析式.
的解析式.
相关知识点
推荐套卷
如图1,在平面直角坐标系中,抛物线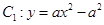 (
(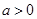 )经过点
)经过点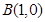 ,顶点为
,顶点为 .
.
(1)求抛物线 的解析式;
的解析式;
(2)如图2,先将抛物线 向上平移使其顶点在原点
向上平移使其顶点在原点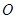 ,再将其顶点沿直线
,再将其顶点沿直线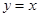 平移得到抛物线
平移得到抛物线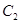 ,设抛物线
,设抛物线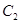 与直线
与直线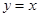 交于
交于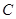 、
、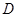 两点,求线段
两点,求线段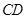 的长.
的长.
(3)在图1中将抛物线 绕点
绕点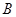 旋转
旋转 后得到抛物线
后得到抛物线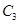 ,直线
,直线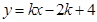 总经过一个定点
总经过一个定点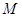 ,若过定点
,若过定点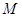 的直线
的直线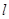 与抛物线
与抛物线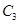 只有一个公共点,求直线
只有一个公共点,求直线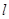 的解析式.
的解析式.