书籍是人类进步的阶梯.联合国教科文组织把每年的4月23日确定为“世界读书日”.某校为了了解该校学生一个学期阅读课外书籍的情况,在全校范围内随机对100名学生进行了问卷调查,根据调查的结果,绘制了统计图表的一部分:
请你根据以上信息解答下列问题:
(1)补全图1、图2;
(2)这100名学生一个学期平均每人阅读课外书籍多少本?若该校共有4000名学生,请你估计这个学校学生一个学期阅读课外书籍共多少本?
(3)根据统计表,求一个学期平均一天阅读课外书籍所用时间的众数和中位数.
相关知识点
推荐套卷
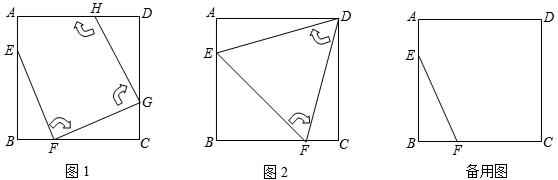
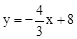 与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s)(0<t≤3).
与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s)(0<t≤3).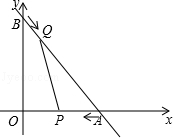
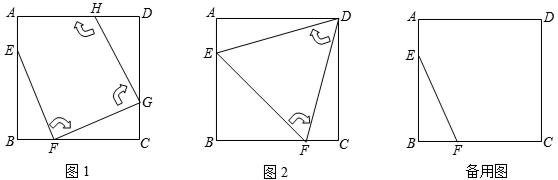
 ,AD=7,AH=
,AD=7,AH=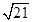 .现有两个动点E、F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动. 在点E、F运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,当点E运动到点C时,E、F两点同时停止运动. 设运转时间为t秒.
.现有两个动点E、F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动. 在点E、F运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,当点E运动到点C时,E、F两点同时停止运动. 设运转时间为t秒. . 在旋转过程中,点E与点C重合,F的对应点为F′,G的对应点为G′. 设直线F′G′与射线DC、射线AC分别相交于M、N两点.试问:是否存在点M、N,使得△CMN是以∠MCN为底角的等腰三角形?若存在,请求出线段CM的长度;若不存在,请说明理由.
. 在旋转过程中,点E与点C重合,F的对应点为F′,G的对应点为G′. 设直线F′G′与射线DC、射线AC分别相交于M、N两点.试问:是否存在点M、N,使得△CMN是以∠MCN为底角的等腰三角形?若存在,请求出线段CM的长度;若不存在,请说明理由.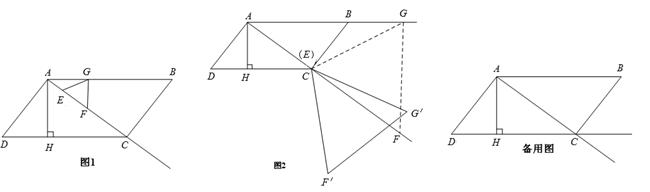
 粤公网安备 44130202000953号
粤公网安备 44130202000953号