在平面直角坐标系中，已知点A（a，0），C（0，b）满足（a+1）2+
=0
（1）直接写出：a= -1，b= -3；
（2）点B为x轴正半轴上一点，如图1，BE⊥AC于点E，交y轴于点D，连接OE，若OE平分∠AEB，求直线BE的解析式；
（3）在（2）条件下，点M为直线BE上一动点，连OM，将线段OM逆时针旋转90°，如图2，点O的对应点为N，当点M的运动轨迹是一条直线l，请你求出这条直线l的解析式．
如图，平面直角坐标系中O为坐标原点，直线
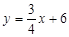与x轴、y轴分别交于A、B两点，C为OA中点；
（1）求直线BC解析式；
（2）动点P从O出发以每秒2个单位长度的速度沿线段OA向终点A运动，同时动点Q从C出发沿线段CB以每秒
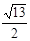个单位长度的速度向终点B运动，过点Q作QM∥AB交x轴于点M，若线段PM的长为y，点P运动时间为t( )，求y于t的函数关系式；
（3）在（2）的条件下，以PC为直径作⊙N，求t为何值时直线QM与⊙N相切.
为培养学生养成良好的“爱读书、读好书、好读书”的习惯，让书籍成为传递文明、传递知识、传递和谐的载体，哈市某中学计划创建中、小型两类班级图书角打造书香校园，已知组建一个中型图书角需科技类书籍80本，人文类书籍50本，共需购书费用860元；组建一个小型图书角需科技类书籍30本，人文类书籍60本，共需购书费用570元，又知每本科技类书籍的价格相同，每本人文类书籍的价格也相同．
(1)求每本科技类书籍和每本人文类书籍的价格分别为多少元?
(2)若该学校计划用不超过20000元的资金组建中、小型两类图书角共30个，求最多组建多少个中型图书角?
某中学组织全体学生参加了“学雷锋”的活动，六年级一班同学统计了该天本班学生打扫街道，去敬老院服务和到社区文艺演出的人数，并做了如下直方图和扇形统计图.请根据该班同学所作的两个图形解答：
（1）六年级一班有多少名学生?
（2）求去敬老院服务的学生人数，并补全直方图的空缺部分;
（3）若六年级有800名学生，估计该年级去敬老院的人数.
已知矩形ABCD的周长为12，E、F、G、H为矩形ABCD的各边中点，若AB=x，四边形EFGH的面积为y．
（1）请直接写出y与x的函数关系式；
（2）根据(1)中的函数关系式,计算当x为何值时，y最大，并求出最大值.
（参考公式：当x=-
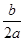时，二次函数y=ax+bx+c(a≠o)有最小(大)值
）
=
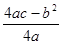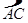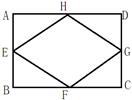
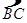，点E为OD上任意一点(不与O、D重合).求证：AE=BE.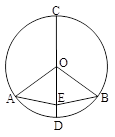
粤公网安备 44130202000953号