已知矩形ABCD的周长为12，E、F、G、H为矩形ABCD的各边中点，若AB=x，四边形EFGH的面积为y．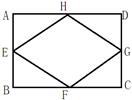
（1）请直接写出y与x的函数关系式；
（2）根据(1)中的函数关系式,计算当x为何值时，y最大，并求出最大值.
（参考公式：当x=-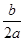
时，二次函数y=ax+bx+c(a≠o)有最小(大)值
）
.
，求
的值．
在同一直线上，
,
，
．
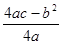．相关知识点
推荐套卷
已知矩形ABCD的周长为12，E、F、G、H为矩形ABCD的各边中点，若AB=x，四边形EFGH的面积为y．
（1）请直接写出y与x的函数关系式；
（2）根据(1)中的函数关系式,计算当x为何值时，y最大，并求出最大值.
（参考公式：当x=-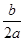时，二次函数y=ax+bx+c(a≠o)有最小(大)值）
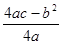粤公网安备 44130202000953号