数列{ a n}满足a 1＋2 a 2＋22 a 3＋…＋2n－1 a n＝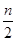
，（n∈N*）前n项和为Sn；数列{bn}是等差数列，且b1=2，其前n项和Tn满足
（
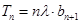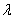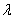为常数，且<1）．
（1）求数列{ a n}的通项公式及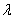的值；
（2）设
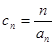，求数列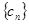
的前n项的和
；
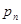（3）证明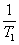
+
+
+ +
>
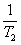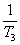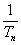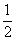Sn．
相关试题
若函数
.
的解析式；
是奇函数，且
.
的值；
在
上的单调性，并用定义加以证明．
，
，
．
，求
，(∁
)
；
，求实数
的取值范围.
过点（0，4），离心率为
的直线被C所截线段的长度.
时，求k的值. 相关知识点
推荐套卷
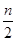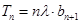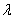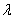数列{ a n}满足a 1＋2 a 2＋22 a 3＋…＋2n－1 a n＝，（n∈N*）前n项和为Sn；数列{bn}是等差数列，且b1=2，其前n项和Tn满足 （为常数，且<1）．
（1）求数列{ a n}的通项公式及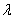的值；
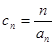（2）设，求数列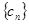的前n项的和；
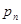（3）证明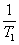++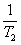+ +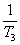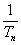>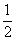Sn．
粤公网安备 44130202000953号