将矩形OABC置于平面直角坐标系中，点A的坐标为（0，4），点C的坐标为（m，0）（m＞0），点D（m，1）在BC上，将矩形OABC沿AD折叠压平，使点B落在坐标平面内，设点B的对应点为点E．
（1）当m=3时，求点B的坐标和点E的坐标；（自己重新画图）
（2）随着m的变化，试探索：点E能否恰好落在x轴上？若能，请求出m的值；若不能，请说明理由．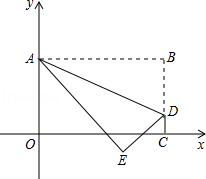
相关试题
位置：
，则点P在. 
，则点P 在 .
，则P在 .
相关知识点
推荐套卷
将矩形OABC置于平面直角坐标系中，点A的坐标为（0，4），点C的坐标为（m，0）（m＞0），点D（m，1）在BC上，将矩形OABC沿AD折叠压平，使点B落在坐标平面内，设点B的对应点为点E．
（1）当m=3时，求点B的坐标和点E的坐标；（自己重新画图）
（2）随着m的变化，试探索：点E能否恰好落在x轴上？若能，请求出m的值；若不能，请说明理由．
粤公网安备 44130202000953号