已知抛物线 G： y＝ mx 2﹣2 mx﹣3有最低点．
（1）求二次函数 y＝ mx 2﹣2 mx﹣3的最小值（用含 m的式子表示）；
（2）将抛物线 G向右平移 m个单位得到抛物线 G 1．经过探究发现，随着 m的变化，抛物线 G 1顶点的纵坐标 y与横坐标 x之间存在一个函数关系，求这个函数关系式，并写出自变量 x的取值范围；
（3）记（2）所求的函数为 H，抛物线 G与函数 H的图象交于点 P，结合图象，求点 P的纵坐标的取值范围．
相关试题
，其中
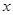为不等式组
的整数解.
如图，在矩形ABCD中，AB＝1，BC＝3，点E为BC边上的动点（点E与点B、C不重合），设BE＝x．
操作：在射线BC上取一点F，使得EF＝BE，以点F为直角顶点、EF为边作等腰直角三角形EFG，设△EFG与矩形ABCD重叠部分的面积为S．
（1）求S与x的函数关系式，并写出自变量x的取值范围；
（2）S是否存在最大值？若存在，请直接写出最大值，若不存在，请说明理由．
如图，正方形ABCD中，AB＝6，点E在边CD上，且CD＝3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．
（1）求证：①△ABG≌△AFG； ②BG＝GC；
（2）求△FGC的面积.
相关知识点
推荐套卷
粤公网安备 44130202000953号