为了解某校学生的视力情况,现采用随机抽样的方式从该校的A,B两班中各抽5名学生进行视力检测.检测的数据如下:
A班5名学生的视力检测结果:4.3,5.1,4.6,4.1,4.9.
B班5名学生的视力检测结果:5.1,4.9,4.0,4.0,4.5.
(1)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?
(2)由数据判断哪个班的5名学生视力方差较大?(结论不要求证明)
(3)现从A班的上述5名学生中随机选取3名学生,用X表示其中视力大于4.6的人数,求X的分布列和数学期望.
相关知识点
推荐套卷
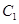 :
: (t为参数),曲线
(t为参数),曲线 :
: 。
。 ;
; ,求
,求 的值.
的值.
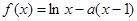 ,
, ∈R.
∈R.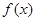 的单调性;
的单调性;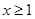 时,
时,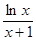 恒成立,求
恒成立,求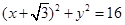 ,点
,点 ,Q是圆上一动点,AQ的垂直平分线交CQ于点M,设点M的轨迹为E。
,Q是圆上一动点,AQ的垂直平分线交CQ于点M,设点M的轨迹为E。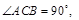
 .
. 平面B1C1D;
平面B1C1D;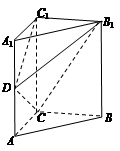
 粤公网安备 44130202000953号
粤公网安备 44130202000953号