已知 、
、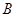 两盒中都有红球、白球,且球的形状、大小都相同,盒子
两盒中都有红球、白球,且球的形状、大小都相同,盒子 中有
中有 个红球与
个红球与 个白球,盒子
个白球,盒子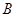 中有
中有 个红球与
个红球与 个白球(
个白球( ).
).
(1)分别从 、
、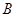 中各取一个球,
中各取一个球,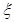 表示红球的个数;
表示红球的个数;
①请写出随机变量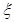 的分布列,并证明
的分布列,并证明 等于定值;
等于定值;
②当 为何值时,
为何值时, 取到最小值,并求出最小值.
取到最小值,并求出最小值.
(2)在盒子 中不放回地摸取3个球,事件
中不放回地摸取3个球,事件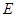 :在第一次取到红球后,以后两次都取到白球,事件
:在第一次取到红球后,以后两次都取到白球,事件 :在第一次取到白球后,以后两次都取到红球,若概率
:在第一次取到白球后,以后两次都取到红球,若概率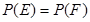 ,求
,求 的值.
的值.
相关知识点
推荐套卷
已知 、
、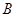 两盒中都有红球、白球,且球的形状、大小都相同,盒子
两盒中都有红球、白球,且球的形状、大小都相同,盒子 中有
中有 个红球与
个红球与 个白球,盒子
个白球,盒子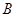 中有
中有 个红球与
个红球与 个白球(
个白球( ).
).
(1)分别从 、
、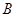 中各取一个球,
中各取一个球,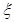 表示红球的个数;
表示红球的个数;
①请写出随机变量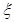 的分布列,并证明
的分布列,并证明 等于定值;
等于定值;
②当 为何值时,
为何值时, 取到最小值,并求出最小值.
取到最小值,并求出最小值.
(2)在盒子 中不放回地摸取3个球,事件
中不放回地摸取3个球,事件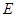 :在第一次取到红球后,以后两次都取到白球,事件
:在第一次取到红球后,以后两次都取到白球,事件 :在第一次取到白球后,以后两次都取到红球,若概率
:在第一次取到白球后,以后两次都取到红球,若概率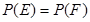 ,求
,求 的值.
的值.