在平面直角坐标系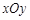
中，已知圆
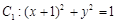，圆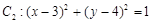
．
（1）若过点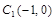
的直线
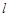被圆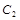
截得的弦长为
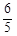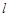，求直线的方程；
（2）圆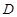
是以1为半径，圆心在圆
：
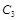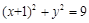上移动的动圆 ，若圆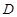上任意一点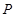
分别作圆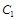
的两条切线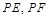
，切点为
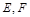，求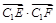
的取值范围 ；
|
（3）若动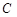圆
同时平分圆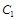的周长、圆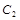的周长，则动圆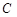是否经过定点？若经过，求出定点的坐标；若不经过，请说明理由．
在
和
附近的平均变化率，并比较它们的大小.
，过原点且倾斜角为
的两条直线分别交椭圆于A、C和B、D两点．（1）用
表示四边形ABCD的面积S；（2）当
时，求S的最大值．
相交于A、B两点，当t变化时，求|AB|的最大值．
的椭圆的中心的轨迹方程
为参数）的准线方程相关知识点
推荐套卷
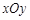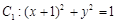在平面直角坐标系中，已知圆，圆．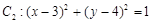
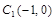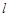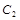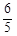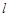（1）若过点的直线被圆截得的弦长为，求直线的方程；
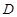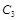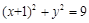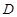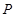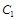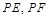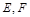（2）圆是以1为半径，圆心在圆：上移动的动圆 ，若圆上任意一点分别作圆 的两条切线，切点为，求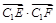的取值范围 ；
|
（3）若动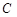圆同时平分圆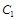的周长、圆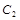的周长，则动圆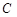是否经过定点？若经过，求出定点的坐标；若不经过，请说明理由．
粤公网安备 44130202000953号