如图，△ABC的顶点坐标分别为A（1，3）、B（4，2）、C（2，1）．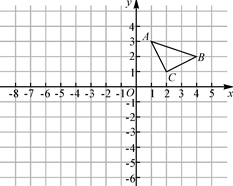
（1）作出与△ABC关于x轴对称的△A1B1C1，并写出点A1的坐标；
（2）以原点O为位似中心，在原点的另一侧画出△A2B2C2，使
＝
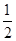，并写出点A2的坐标。
相关试题
，并从0≤x≤2中选一个你认为合适的整数x代入求值．
，求
的值．
．
．相关知识点
推荐套卷
如图，△ABC的顶点坐标分别为A（1，3）、B（4，2）、C（2，1）．
（1）作出与△ABC关于x轴对称的△A1B1C1，并写出点A1的坐标；
（2）以原点O为位似中心，在原点的另一侧画出△A2B2C2，使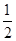＝，并写出点A2的坐标。
粤公网安备 44130202000953号