甲、乙两容器中分别盛有两种浓度的某种溶液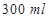
，从甲容器中取出
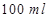溶液，将其倒入乙容器中搅匀，再从乙容器中取出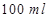溶液，将其倒入甲容器中搅匀，这称为是一次调和，已知第一次调和后，甲、乙两种溶液的浓度分别记为：
，
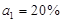，第
次调和后的甲、乙两种溶液的浓度分别记为：
、
.
（1）请用、
分别表示和
；
（2）问经过多少次调和后，甲乙两容器中溶液的浓度之差小于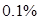
.
相关试题
，
，
，求
；
，求实数a的取值范围．
是定义在
上的增函数，对于任意的
，都有
，且满足
．
的值;
的
的取值范围．
满足条件
，及
．
上的最值．
处的的切线方程；
，求切线方程．
且
，
的值；
在
上的单调性，并用定义给予证明．相关知识点
推荐套卷
甲、乙两容器中分别盛有两种浓度的某种溶液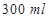，从甲容器中取出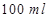溶液，将其倒入乙容器中搅匀，再从乙容器中取出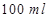溶液，将其倒入甲容器中搅匀，这称为是一次调和，已知第一次调和后，甲、乙两种溶液的浓度分别记为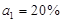：，，第次调和后的甲、乙两种溶液的浓度分别记为：、.
（1）请用、分别表示和；
（2）问经过多少次调和后，甲乙两容器中溶液的浓度之差小于.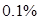
粤公网安备 44130202000953号