某公司为招聘新员工设计了一个面试方案:应聘者从 道备选题中一次性随机抽取
道备选题中一次性随机抽取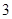 道题,按照题目要求独立完成.规定:至少正确完成其中
道题,按照题目要求独立完成.规定:至少正确完成其中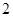 道题的便可通过.已知
道题的便可通过.已知 道备选题中应聘者甲有
道备选题中应聘者甲有 道题能正确完成,
道题能正确完成,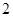 道题不能完成;应聘者乙每题正确完成的概率都是
道题不能完成;应聘者乙每题正确完成的概率都是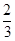 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性大?
相关知识点
推荐套卷
某公司为招聘新员工设计了一个面试方案:应聘者从 道备选题中一次性随机抽取
道备选题中一次性随机抽取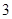 道题,按照题目要求独立完成.规定:至少正确完成其中
道题,按照题目要求独立完成.规定:至少正确完成其中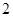 道题的便可通过.已知
道题的便可通过.已知 道备选题中应聘者甲有
道备选题中应聘者甲有 道题能正确完成,
道题能正确完成,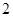 道题不能完成;应聘者乙每题正确完成的概率都是
道题不能完成;应聘者乙每题正确完成的概率都是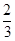 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性大?