【2015高考湖南,理20】已知抛物线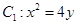 的焦点
的焦点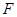 也是椭圆
也是椭圆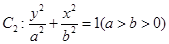 的一个焦点,
的一个焦点,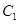 与
与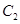 的公共弦的长为
的公共弦的长为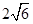 .
.
(1)求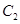 的方程;
的方程;
(2)过点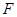 的直线
的直线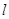 与
与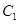 相交于
相交于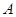 ,
,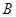 两点,与
两点,与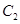 相交于
相交于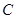 ,
,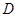 两点,且
两点,且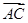 与
与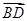 同向
同向
(ⅰ)若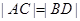 ,求直线
,求直线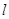 的斜率
的斜率
(ⅱ)设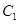 在点
在点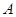 处的切线与
处的切线与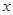 轴的交点为
轴的交点为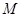 ,证明:直线
,证明:直线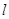 绕点
绕点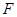 旋转时,
旋转时,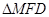 总是钝角三角形
总是钝角三角形
推荐套卷
【2015高考湖南,理20】已知抛物线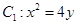 的焦点
的焦点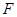 也是椭圆
也是椭圆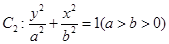 的一个焦点,
的一个焦点,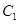 与
与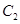 的公共弦的长为
的公共弦的长为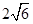 .
.
(1)求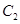 的方程;
的方程;
(2)过点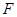 的直线
的直线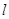 与
与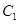 相交于
相交于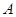 ,
,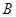 两点,与
两点,与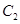 相交于
相交于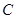 ,
,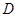 两点,且
两点,且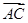 与
与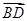 同向
同向
(ⅰ)若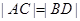 ,求直线
,求直线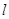 的斜率
的斜率
(ⅱ)设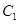 在点
在点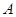 处的切线与
处的切线与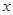 轴的交点为
轴的交点为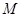 ,证明:直线
,证明:直线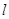 绕点
绕点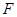 旋转时,
旋转时,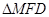 总是钝角三角形
总是钝角三角形