【2015高考新课标1，理20】在直角坐标系
中，曲线C：y=
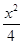与直线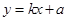
（
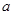＞0）交与M,N两点，
（Ⅰ）当k=0时，分别求C在点M和N处的切线方程；
（Ⅱ）y轴上是否存在点P，使得当k变动时，总有∠OPM=∠OPN？说明理由．
相关试题
是单位圆
上的点，点
是单位圆与
轴正半轴的交点，点
在第二象限．记
且
．
的值．
的不等式
的解集是空集，求实数
的取值范围
都是正数．
，求
的最大值；
，求
的最小值．
．
的单调递增区间；
的方程
在
]上有两个不同的解，求实数
的取值范围．推荐套卷
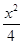【2015高考新课标1，理20】在直角坐标系中，曲线C：y=与直线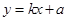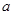（＞0）交与M,N两点，
（Ⅰ）当k=0时，分别求C在点M和N处的切线方程；
（Ⅱ）y轴上是否存在点P，使得当k变动时，总有∠OPM=∠OPN？说明理由．
粤公网安备 44130202000953号