【2015高考上海,理21】已知椭圆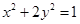 ,过原点的两条直线
,过原点的两条直线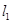 和
和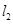 分别于椭圆交于
分别于椭圆交于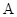 、
、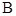 和
和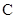 、
、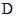 ,记得到的平行四边形
,记得到的平行四边形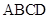 的面积为
的面积为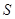 .
.
(1)设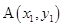 ,
,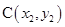 ,用
,用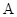 、
、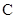 的坐标表示点
的坐标表示点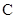 到直线
到直线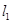 的距离,并证明
的距离,并证明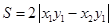 ;
;
(2)设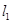 与
与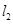 的斜率之积为
的斜率之积为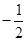 ,求面积
,求面积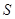 的值.
的值.
推荐套卷
【2015高考上海,理21】已知椭圆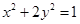 ,过原点的两条直线
,过原点的两条直线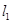 和
和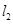 分别于椭圆交于
分别于椭圆交于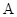 、
、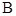 和
和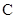 、
、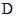 ,记得到的平行四边形
,记得到的平行四边形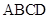 的面积为
的面积为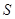 .
.
(1)设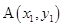 ,
,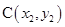 ,用
,用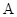 、
、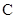 的坐标表示点
的坐标表示点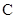 到直线
到直线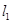 的距离,并证明
的距离,并证明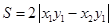 ;
;
(2)设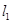 与
与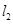 的斜率之积为
的斜率之积为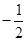 ,求面积
,求面积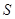 的值.
的值.