已知数列{an}的前n项和为Sn，且Sn＝2an－2，数列{bn}满足b1＝1，且bn＋1＝bn＋2.
(1)求数列{an}，{bn}的通项公式；
(2)设cn＝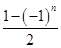
an－
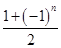bn，求数列{cn}的前2n项和T2n.
相关试题
，
的等比中项。
是等差数列；（2）若
的前n项和为Tn,求Tn。
的值；（2）若
的值。
图象的对称中心的横坐标；
，求函数
的定义域为集合A,函数
的定义域为集合B.
A，求实数
的取值范围。
（
）.
的单调区间；
在
内有且只有一个极值点, 求a的取值范围.相关知识点
推荐套卷
已知数列{an}的前n项和为Sn，且Sn＝2an－2，数列{bn}满足b1＝1，且bn＋1＝bn＋2.
(1)求数列{an}，{bn}的通项公式；
(2)设c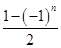n＝an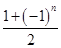－bn，求数列{cn}的前2n项和T2n.
粤公网安备 44130202000953号