我们不妨约定:在平面直角坐标系中,若某函数图象上至少存在不同的两点关于
轴对称,则把该函数称之为“
函数”,其图象上关于
轴对称的不同两点叫做一对“
点”.根据该约定,完成下列各题.
(1)若点
与点
是关于
的“
函数”
的图象上的一对“
点”,则
,
,
(将正确答案填在相应的横线上);
(2)关于
的函数
,
是常数)是“
函数”吗?如果是,指出它有多少对“
点”如果不是,请说明理由;
(3)若关于
的“
函数”
,且
,
,
是常数)经过坐标原点
,且与直线
,
,且
,
是常数)交于
,
,
,
两点,当
,
满足
时,直线
是否总经过某一定点?若经过某一定点,求出该定点的坐标;否则,请说明理由.
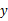 轴交于点B,且OA=OB,求这两个函数的关系式及两直线与
轴交于点B,且OA=OB,求这两个函数的关系式及两直线与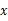 轴围成的三角形的面积.
轴围成的三角形的面积. 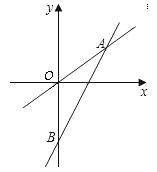
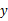 轴交于点B,且OA=OB,求这两个函数的关系式及两直线与
轴交于点B,且OA=OB,求这两个函数的关系式及两直线与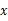 轴围成的三角形的面积.
轴围成的三角形的面积. 