设无穷数列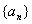 的首项
的首项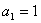 ,前
,前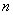 项和为
项和为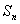 (
(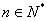 ),且点
),且点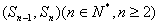 在直线
在直线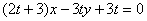 上(
上(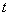 为与
为与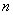 无关的正实数).
无关的正实数).
(1)求证:数列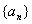 (
(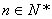 )为等比数列;
)为等比数列;
(2)记数列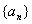 的公比为
的公比为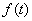 ,数列
,数列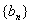 满足
满足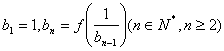 ,设
,设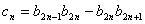 ,求数列
,求数列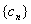 的前
的前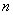 项和
项和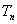 ;
;
(3)若(2)中数列{Cn}的前n项和Tn当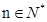 时不等式
时不等式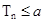 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
推荐套卷
设无穷数列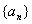 的首项
的首项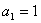 ,前
,前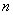 项和为
项和为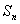 (
(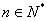 ),且点
),且点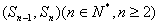 在直线
在直线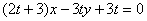 上(
上(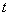 为与
为与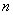 无关的正实数).
无关的正实数).
(1)求证:数列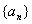 (
(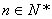 )为等比数列;
)为等比数列;
(2)记数列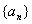 的公比为
的公比为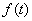 ,数列
,数列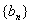 满足
满足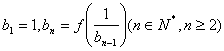 ,设
,设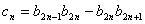 ,求数列
,求数列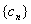 的前
的前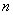 项和
项和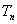 ;
;
(3)若(2)中数列{Cn}的前n项和Tn当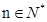 时不等式
时不等式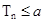 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。