已知
是数列
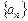的前n项和，满足关系式
，
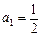
（n≥2，n为正整数）.
（1）令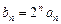
，证明：数列
是等差数列；
（2）求数列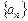的通项公式；
（3）对于数列
，若存在常数M＞0，对任意的
，恒有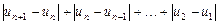
≤M成立，称数列为“差绝对和有界数列”，
证明：数列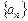为“差绝对和有界数列”.
的底面是边长为1的正方形，
平面
是平行四边形
所在平面外一点，
、
分别是
、
的中点； 求证：
平面
平面
，
直线
，则
平面
经过平面
内一定点
，但
.（填所选条件的序号）推荐套卷
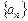已知是数列的前n项和，满足关系式，
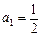
（n≥2，n为正整数）.
（1）令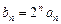，证明：数列是等差数列；
（2）求数列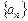的通项公式；
（3）对于数列，若存在常数M＞0，对任意的，恒有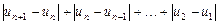≤M成立，称数列为“差绝对和有界数列”，
证明：数列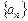为“差绝对和有界数列”.
粤公网安备 44130202000953号