如图,PA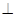 平面ABCD,四边形ABCD为矩形,PA=AB=
平面ABCD,四边形ABCD为矩形,PA=AB=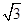 ,AD=1,点F是PB的中点,点E在边BC上移动.
,AD=1,点F是PB的中点,点E在边BC上移动.
(I)求三棱锥E—PAD的体积;
(II)试问当点E在BC的何处时,有EF//平面PAC;
(1lI)证明:无论点E在边BC的何处,都有PE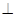 AF.
AF.
推荐套卷
如图,PA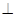 平面ABCD,四边形ABCD为矩形,PA=AB=
平面ABCD,四边形ABCD为矩形,PA=AB=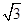 ,AD=1,点F是PB的中点,点E在边BC上移动.
,AD=1,点F是PB的中点,点E在边BC上移动.
(I)求三棱锥E—PAD的体积;
(II)试问当点E在BC的何处时,有EF//平面PAC;
(1lI)证明:无论点E在边BC的何处,都有PE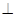 AF.
AF.