[山东]2014届山东省德州市高三上学期期末考试文科数学试卷
已知集合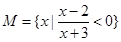 ,集合N={
,集合N={ },则M
},则M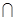 N为
N为
| A.(-2,3) | B.(-3,-2] | C.[-2,2) | D.(-3,3] |
已知a,b,c,d为实数,且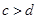 ,则“
,则“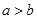 ”是“
”是“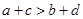 ”的
”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
某工厂对一批产品进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[l04,l06].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于102克的产品的个数是
| A.90 | B.75 | C.60 | D.45 |
某算法的程序框图如图所示,如果输出的结果是26,则判断框内应为
| A.K>1 | B.K>2 |
| C.K>3 | D.K>4 |
函数y=sin2x的图象向右平移 个单位,得到的图象关于直线
个单位,得到的图象关于直线 对称,则
对称,则 的最小值为
的最小值为
A. |
B. |
C. |
D. |
已知平行四边形ABCD中,AC为一条对角线,若 =(2,4),
=(2,4), =(1,3),则
=(1,3),则 =
=
A. 8 8 |
B. 6 6 |
C.6 | D.8 |
设 、
、 是两个不重合的平面,m、m是两条不重合的直线,则以下结论错误的是
是两个不重合的平面,m、m是两条不重合的直线,则以下结论错误的是
A.若 ,则 ,则 |
B.若 ,则 ,则 |
C.若 ,则 ,则 |
D.若 ,则 ,则 |
已知双曲线C1: 的离心率为2,若抛物线C2:
的离心率为2,若抛物线C2: 的焦点到双曲线C1的渐近线的距离是2,则抛物线C2的方程是
的焦点到双曲线C1的渐近线的距离是2,则抛物线C2的方程是
A. |
B. |
C. |
D. |
没函数 在(0,+
在(0,+ )内有定义,对于给定的正数K,定义函数
)内有定义,对于给定的正数K,定义函数 ,取函数
,取函数 ,恒有
,恒有 ,则
,则
A.K的最大值为 |
B.K的最小值为 |
| C.K的最大值为2 | D.K的最小值为2 |
已知圆的方程为 .设该圆过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为 .
.设该圆过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为 .
某校从参加市联考的甲、乙两班数学成绩110分以上的同学中各随机抽取8人,将这l6人的数学成绩编成茎叶图,如图所示.
(I)茎叶图中有一个数据污损不清(用△表示),若甲班抽出来的同学平均成绩为l22分,试推算这个污损的数据是多少?
(Ⅱ)现要从成绩在130分以上的5位同学中选2位作数学学习方法介绍,请将所有可能的结果列举出来,并求选出的两位同学不在同一个班的概率.
已知a,b,c分别为 ABC的三个内角A,B,C的对边,
ABC的三个内角A,B,C的对边, =(sinA,1),
=(sinA,1), =(cosA,
=(cosA, ),且
),且 //
// .
.
(I)求角A的大小;
(II)若a=2,b=2 ,求
,求 ABC的面积.
ABC的面积.
如图,PA 平面ABCD,四边形ABCD为矩形,PA=AB=
平面ABCD,四边形ABCD为矩形,PA=AB= ,AD=1,点F是PB的中点,点E在边BC上移动.
,AD=1,点F是PB的中点,点E在边BC上移动.
(I)求三棱锥E—PAD的体积;
(II)试问当点E在BC的何处时,有EF//平面PAC;
(1lI)证明:无论点E在边BC的何处,都有PE AF.
AF.
已知数列{ }中,
}中, ,前n项和
,前n项和 .
.
(I)求a2,a3以及{ }的通项公式;
}的通项公式;
(II)设 ,求数列{
,求数列{ }的前n项和Tn.
}的前n项和Tn.
设函数 ,曲线
,曲线 通过点(0,2a+3),且在
通过点(0,2a+3),且在 处的切线垂直于y轴.
处的切线垂直于y轴.
(I)用a分别表示b和c;
(II)当bc取得最大值时,写出 的解析式;
的解析式;
(III)在(II)的条件下,若函数 g(x)为偶函数,且当
g(x)为偶函数,且当 时,
时, ,求当
,求当 时g(x)的表达式,并求函数g(x)在R上的最小值及相应的x值.
时g(x)的表达式,并求函数g(x)在R上的最小值及相应的x值.
 满足
满足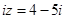 (
(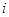 为虚数单位),则
为虚数单位),则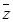 为
为
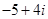


 的零点所在的区间为
的零点所在的区间为 的图象的大致形状是
的图象的大致形状是
 满足约束条件
满足约束条件 ,若
,若 ,则实数
,则实数 的取值范围为 .
的取值范围为 .
 ; ②
; ② ;
; ;④
;④ .
. ,若椭圆C的一个焦点为F(
,若椭圆C的一个焦点为F( ,0),其短轴上的一个端点到F的距离为
,0),其短轴上的一个端点到F的距离为 .
. 且
且 =0,其中N为椭圆的下顶点,求直线在y轴上截距的取值范围.
=0,其中N为椭圆的下顶点,求直线在y轴上截距的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号