设函数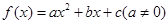
，曲线
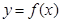通过点(0，2a+3)，且在
处的切线垂直于y轴．
(I)用a分别表示b和c；
(II)当bc取得最大值时，写出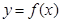的解析式；
(III)在(II)的条件下，若函数
g(x)为偶函数,且当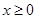
时,
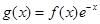，求当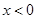
时g(x)的表达式，并求函数g(x)在R上的最小值及相应的x值．
相关试题
，当
时，其前
项和
满足
；
，求数列｛
｝的前项和
有相同的焦点，且椭圆过点
，
过点
交椭圆于
两点，且
，求直线
中，
∠
=90°，
，
⊥
.
（Ⅰ）求证：
；
的体积.
中，已知
，
，
．
（1）求
的值；（2）求
的值．
表示事件“抽到两 题的编号分别为
,且
＜
”。
（1）共有多少个基本事件？并列举出来。相关知识点
推荐套卷
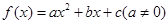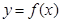设函数，曲线通过点(0，2a+3)，且在处的切线垂直于y轴．
(I)用a分别表示b和c；
(II)当bc取得最大值时，写出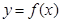的解析式；
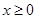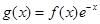(III)在(II)的条件下，若函数g(x)为偶函数,且当时,，求当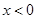时g(x)的表达式，并求函数g(x)在R上的最小值及相应的x值．
粤公网安备 44130202000953号